第6回 偏相関係数と因果効果
第6回 偏相関係数と因果効果
心理学実験で因果関係を知る方法について解説する。因果関係を知るにはどうすればいいか、具体的にどのようにデータを取得すればいいのかについて理解することを目指す。
【キーワード】
因果推論、疑似相関、交絡、共変量、偏相関係数、統制群と実験群、無作為割当、平均因果効果
6.1 因果関係とは
6.2 擬似相関と相関関係数
6.3 無作為割り当て実験による因果関係の検証
6.4 まとめ
6.1 因果関係とは
スイッチ(原因) → 明かりがつく(結果)
■心理学の因果関係
・ある行動が生じる原因は何か
・発達や心の変化が生じる原因は何か
6.1.因果関係を統計学で知るための表現方法
原因 変数X
結果 変数Y
6.2 因果関係を調べるための条件
ジョン・スチュアート・ミルによる条件
1.原因Xが結果Yよりも時間的に先行していること
2.原因Xが結果Yよりも共編関係にあること
3.他の因果的説明が排除されていること
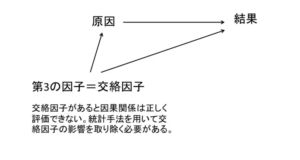
6.2 擬似相関と相関関係数
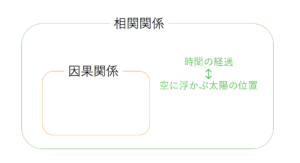
相関関係が見られても、それが因果関係ではない可能性があること
共変数と呼ばれる第三の変数の存在によって、相関関係の値が変化しうること
6.2.1 層別の相関係数
6.2.2 共変数による相関係数の変化と擬似相関
擬似相関(ぎじそうかん、英: Spurious relationship, Spurious correlation)は、2つの事象に因果関係がないのに、見えない要因(潜伏変数)によって因果関係があるかのように推測されること。擬似相関は、客観的に精査するとそれが妥当でないときにも、2つの集団間に意味の有る関係があるような印象を与える。
6.2.3 偏相関関係
・層ごとに分析は可能
・しかし、連続的な共変量の場合はどうするか?
■偏相関係数
・共変量が変数Xと変数Yと両方相関していることを考慮する
・共変量の値が一定のときの変数Xと変数Yの間の相関係数を推定する。
6.2.4 偏相関関係と因果関係
6.3 無作為割り当て実験による因果関係の検証
原理的にあらゆる共変量と相関がない状態で因果関係を推定することができる無作為割り当て実験
6.3.1 統計的因果推論
反事実モデルと呼ばれる因果推論(causal inference)
因果効果(causal effect)、処置効果(treatment effect)
6.3.2 無作為割り当て実験と平均因果効果
無作為割り当て:
平均因果効果(average causal effect):個人ではなく、集団の因果効果のこと
6.3.3 平均因果効果の大きさを表す指標
標準化効果量(standerdized effect size): 平均の差についての相関係数のように標準化された効果についての指標
Cohenが提案したdという指標
6.4 まとめ
相関係数だけでは、共変数との交絡の可能性があるため、因果関係を推定することはできない。
偏相関係数によって共変数を統制する必要がある。
あるいは、無作為割り当てによってあらゆる交絡を無くす方法も有効です。