第11回　２条件の平均値の差の推定

第11回　２条件の平均値の差の推定
心理学の研究において利用される頻度の高い、２条件の平均値の差の推定について解説する。データに対応がない場合と対応がある場合についてそれぞれ、２条件の平均値の差の区間推定および標準化平均値差の区間推定について解説する。
【キーワード】
２条件の平均値の差、標準化平均値差、区間推定

平均値の差の可視化と数値要約
母集団における平均値の差の推定
標準化平均値差とその推定
対応のある場合における平均値差の推定

11.1 心理学における平均値の差の推定

平均値差を検討する場合の関心→統制条件と実験条件で従属変数の値にどの程度の差があるか

実験操作を無作為に与えることで、条件間の平均値差を集団レベルの因果関係として解釈することができる。(第6回)→研究者が興味をもっている因果効果について知ることができるため心理学の研究でよく使用されている。

11.2 平均値の差の可視化と数値要約

標本

平均値差　　y1 – y2 =113-101=12

平均因果効果 「外向きの矢羽根は、主観的な長さを12mm過大視させる効果を持つ」

11.3 母集団における平均値の差の推定

母集団における平均値差μ1 – μ2の推定量として標本平均値差y1 – y2 を利用する。

点推定　　得られたデータから1つの値で推定

区間推定　得られたデータから一定の区間で推定(95%信頼区間)

標本抽出による標本平均値差の変動を考慮して、幅を持たせて推定する。

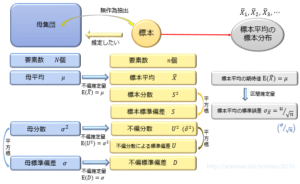
11.3.1 標本平均値差の標本分布

2条件で等しいと仮定した母分散(σ²)が不明　→　母分散に依存しない統計量を計算する。

1変数の母平均推定(第9回)の内容と関連。

平均値差については、自由度n1+n2-2のt分布に従うことを利用

11.3.2 平均値差の点推定

母集団における平均値差の点推定値は、標本を抽出するたびに異なります。

11.3.3 平均値差の区間推定

平均値差の95%信頼区間を求める方法

t分布は0を中心に左右対称なので、下側確率2.5%点と上側確率2.5%点の絶対値は同じ

11.4 標準化平均値差

11.4.1標本における標準化平均値差

平均値差が標準偏差の何個分離れているかを示す指標→測定単位に依存しないため、解釈されやすい。

Cohenのd

母集団における標準化平均値差δ(デルタ)の推定量としてdを利用

δの区間推定は非心t分布を利用する必要がある。

11.5対応のある場合における平均値差の推定

11.5.1対応のない場合と対応のある場合

カウンターバランスという手法を用いたりする。

11.5.2 対応のある場合の平均値差

Tweet

Pocket