数学は役に立たないと思う人が知らない”真実” その人が｢勉強の役立て方｣を知らないだけだ
社会人になると、日常的に触れることが少ない数学。しかし、数学の知識があれば、何気ない出来事も違った見え方がするようです。
数字の魅力や難問から基礎問題の解き方を発信している、数学クリエイターあきとんとんさんの著書『見るだけで理解が加速する 得点アップ 数学公式図鑑』から一部抜粋してお届けします。
スマホゲームなどで、1／100の確率でレア（当たり）が当たるガチャがあるとします。このガチャを100回引くと、必ずレアが当たると思いますか？
もし、ここで、Yesと思ったのであれば、スマホゲームは向いてないかもしれません。なぜなら、この質問の答えはNoだからです。1／100の確率でレアが当たるガチャを引いても、必ずレアが当たるわけではありません。
現実世界のガチャとスマホガチャの違い
前提条件として、現実世界のいわゆるガチャガチャ、ガチャポン（正式名称：カプセルトイ）では1回引くと中にある商品が減ります。したがって、最初に100個の商品があり、その中に1つ当たりがあるガチャガチャであれば、100回引いたら必ずレアは当たります。なぜなら中にあるものをすべて手に入れられるわけですから。
ただし、 “スマホゲーム”のガチャではこの条件が変わります。最近では減る設定をするゲームもあるようですが、空想上のガチャでは基本的に、1回引くたびに中にある商品は減りません。したがって、100個中1個当たりがあったとして、1回引いてハズレが出てもガチャの状態は最初の“100個中1個当たり”から変わらないのです。
現実では、1回引いてハズレなら次は、99個中1個当たりがあるという状態です。これを数学的に見ていくと、当たりが出る確率は1／100→1／99というように大きくなっていき、1に近づいていき、必ず当たりが出る状況になります。
それでは、なぜスマホゲームでは必ずレアが当たらないのかの感覚的なことはわかったと思うので、スマホゲームでは1／100の確率でレアが当たるガチャを100回引いた場合は何％の確率でレアが当たるのか計算してみましょう。
ここで使う知識は、“余事象”というものです。つまり、「100回引いて1回レアが当たる確率」を直接求めるのではなく、「100回引いて、100回ハズレの確率」を求めてから、1から引きます。
全体で100個のものがあり、その中に1個レアがあるガチャを考えます。この場合、レアが出る確率は、
1／100
なので、レアが出ない確率は、
99／100
それが100回連続で起こる確率は、
（99／100）100
なので、1からこれを引くと……
1-（99／100）100≒0.634
となります。つまり、1／100の確率でレアが当たるガチャを引いて、1回レアが当たる確率は約63%ということが、数学的にわかります。想像よりも、ずっと低いと思いませんか？
この記事を読んだみなさんは、スマホゲームでガチャを引くときは確率を考えてから引いてみてください。
数学で0で割ったらダメだ！と言われる理由
次に、多くの方が小学生のときに多くの人が経験したであろう、以下の疑問についてお話しします。
「どうして0で割り算してはいけないのだろう？」
これについても、数学的な観点からお話しさせていただきます。というのも、もし0で割ることができたら、数学的にはすごく不思議な世界が成り立つのです。
0=0
＝（イコール）というのは、このように同じ数字をでつなげますよね。次に、以下のように見方を変えましょう。
9-9=12-12
これも先ほどと同じで、結果が0=0になるので、同じ数字を＝でつないでいる形になります。そうしたら、次にこの式を以下のように分解します。
3×3-3×3=3×4-3×4
次にこの式を、左辺は3、右辺は4でくくると以下のようになります。
3（3-3）=4（3-3）
これを展開したらもとに戻るので、同じ式ということがわかりますよね。次に、両辺が（3-3）と同じ数があるので、（3-3）で割ります。すると、以下のようになります。
3=4
どうでしょうか。＝は同じ数をつなげるのにもかかわらず、3と4が同じという結果になっています。どこかでしてはいけないことをしているのですが、わかりますか？
そうです。両辺を（3-3）で割ってしまっている点です。3-3=0なので、ここでは0で割っていることと同じになります。
つまり、0で割ることを許してしまうと、3=4のような不思議な世界が成り立ってしまいます。これは、別に3=4でなくても成り立ちます。例えば次のような方程式は成り立ちますよね。
10000×0=1×0
これは計算すると、0=0となります。
ところが、計算をするまえに両辺の「×0」が共通なので、両辺を0で割ります。すると、以下のようになります。
10000=1
どうでしょうか。小学生のときに学校で「0で割ったらダメ！」と習ったのは、こういったことが起こらないようにルールを作成しているのです。
270度の三角形が存在する考え方
最後にお話するのは、「三角形の内角の和は180度」という“決まり”についてです。
小学校〜高校では、三角形の内角の和は180度と習います。そして、それが所謂、「普通」だと思います。しかし、大学で数学を勉強していくと、270度の三角形というのが出てきます。「おいおいおいマジか！？」ってなりませんか？
簡単に説明すると、三角形とは、直線を点と点を結んだ最短距離と定義すると、3直線で囲まれた図形のことです。そして、180度の三角形は、平面上の3線で囲まれた図形のことです。これを平面ではなくて、球面上で考えます。すると下図のようになります。
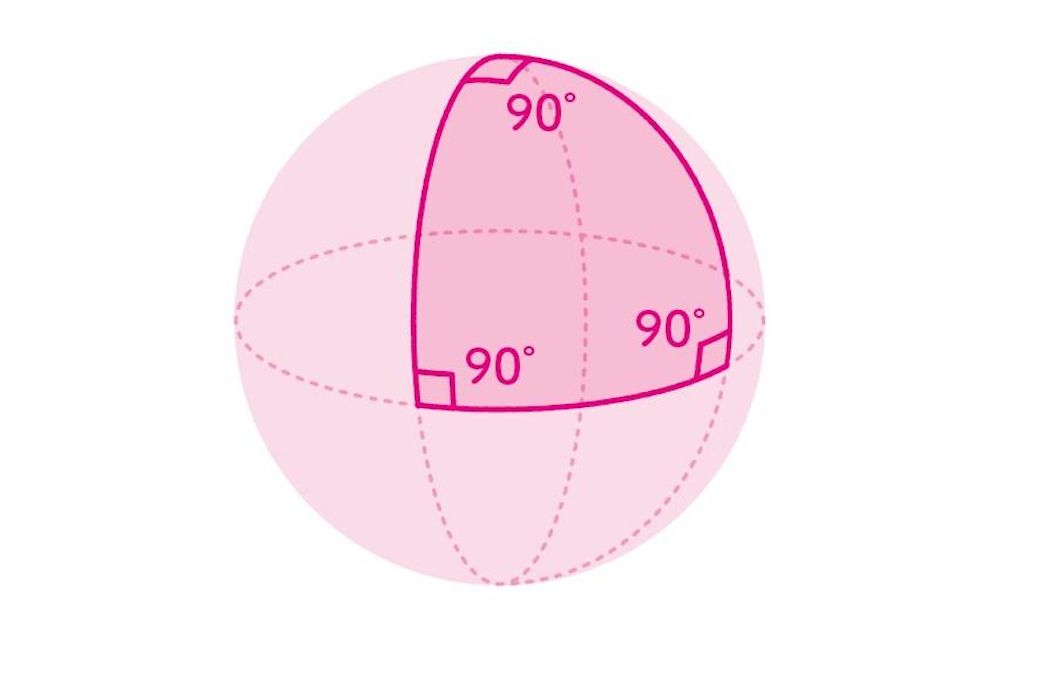高校生は習わない、内角の和が270度の三角形（出所：『見るだけで理解が加速する 得点アップ 数学公式図鑑』）
面白くないですか？ こんな風に球面上で考えると、180度以上の三角形の可能性が考えられます。これは2点を最短距離で結んでますよね。身近で考えると飛行機のフライトとかでも、地球上空を直線距離で飛行していますよね。
ほかにも、球面上で考えると、2角形が作れたり、平行線が交わったりと今まで習っていた数学が覆ることがあります。こういった数学を非ユークリッド幾何学といいます。
注意点として、これを読んでいる中学生・高校生は学校で習う三角形は内角の和は180度であり、2角形など作れず、平行線は交わらないと覚えて数学に取り組んでいてください。この270度の三角形の話は、大学でも数学にトライする際に、深く学んでいただければと思います。
数学に限ったことではないですが、勉強は大人になって働いたり、普通に過ごすなかでも役立てることができます。「勉強は役に立たない」と言う人の多くは、役立て方を知らないだけなのです。大人になってからも勉強を続けて、いろんな所でその成果を役立てていただけると幸いです。
著者：あきとんとん
