50000番小惑星「クワオアー」に「環」を発見! 環をロシュ限界の外側で初めて発見
土星に代表されるように、太陽系の天体の幾つかは環を持っています。当初、環は4つの巨大惑星、すなわち木星・土星・天王星・海王星でのみ知られていたため、天体が環を持つにはある程度の大きさが必要であると考えられてきました。しかし、2014年にケンタウルス族の小惑星カリクローで環が発見されたことで、小さな天体にも環が存在することが実証されました。その後も小天体の環の発見は相次ぎ、現在では小惑星のキロンと準惑星のハウメアでも環が発見されています。
小さな天体の環は極めて細く暗いため、望遠鏡で直接観測を行うことはできず、環を見つけるには「星食」を観測する必要があります。小惑星が恒星の手前を横切ると、地球からは恒星が小惑星に隠されることで、一時的に消えたように見えます。これが星食と呼ばれる現象です。環を持たない天体が横切る場合に恒星が消えるのは1回だけですが、環を持つ天体の場合は本体の1回に加えて環が2回、本体の前後に横切ることになります。恒星が消えたように見えたタイミングや継続時間を厳密に測ることで、環から天体までの距離、環の幅や本数といった情報を得ることができます。星食は滅多に起こる現象ではなく、事前に環の存在を知る手段が存在しないことから、ある天体に環が見つかるかどうかは偶然によります。
リオデジャネイロ連邦大学のB. E. Morgado氏などの国際研究チームは、2018年から2021年にかけて、50000番小惑星「クワオアー」の星食の観測を行いました。クワオアーの推定直径は1110kmで、その大きさや軌道の性質から準惑星の候補天体でもあります。これまでにクワオアーは直径約170kmの衛星「ウェイウォット」を持つことが判明しているものの、物理的性質の多くはわかっていません。星食を観測すれば、正確な直径の値や大気の有無など、クワオアーの様々な性質を知ることができると期待されます。ただし、クワオアーの星食は1分もかからないほど短いイベントであり、正確な計測には高感度の観測装置が必要となります。そこで研究チームは、スペイン領カナリア諸島ラ・パルマ島にあるロケ・デ・ロス・ムチャーチョス天文台の「カナリア大望遠鏡」に、シェフィールド大学が開発した超高感度高速カメラ「HiPERCAM」を取りつけて、クワオアーの星食イベントを観測しました。
【▲ 図1: クワオアーと衛星ウェイウォット、そして環の想像図(Credit: ESA)】
そして予想外なことに、クワオアーの星食では3回の減光が観測されました。先述の通り、このような減光現象は環に由来する可能性が高いと言えます。複数回の観測により、クワオアーは公転半径4100kmの環を持つと推定されました。これにより、クワオアーは太陽系内で環を持つ8番目の天体となったのです (※) 。
※…本研究の論文およびプレスリリースではキロンの環がカウントされていないため、その場合は7番目の天体となります。しかし、筆者が調べる限りではキロンの環の存在が明確に否定されたという根拠が見つからなかったため、本記事では環を持つ天体としてカウントしています。なお、かつて環が存在すると主張されたものの、その後の観測で明確に否定された天体には、土星の衛星レアと準惑星の冥王星があります。
【▲ 図2: 太陽系で知られている環を持つ天体の一覧(Credit: 彩恵りり)】
ただし、クワオアーの環は他の天体の環と異なる性質を持ちます。環の公転半径約4100kmはクワオアーの半径の7.4倍ですが、これはクワオアーの「ロシュ限界」のはるかに外側です。ロシュ限界とは、ある天体を公転する衛星の大きさを制限する値です。主星の周りを公転する天体は、主星から潮汐力を受けます。潮汐力の大きさは公転する天体が大きく、主星に近いほど大きくなります。そのため、主星にあまりに近いと、ある程度の大きさを持つ天体は潮汐力で砕けてしまうため、存在できないことになります。この限界となる距離をロシュ限界と呼びます (※) 。
※…環の見つかっている巨大惑星には、ロシュ限界の内側にいくつかの衛星が見つかっています。ロシュ限界で実際に天体が砕けるかどうかは天体の大きさや密度にも依存するため、小さく低密度な衛星はロシュ限界でも存在することができると考えられています。
これまで見つかった環は、いずれもロシュ限界の内側や境界部に存在するか、そうであると推定されるため、環は潮汐力によって衛星になれない物質の集合体であると見なされていました。裏を返せば、ロシュ限界の外側では物質が集まって衛星が形成されるため、環は存在しないという意味になります。しかし今回、クワオアーで発見された環はロシュ限界のはるか外側にあるため、この理論に反する存在となります。
【▲ 図3: クワオアーの環はロシュ限界 (Roche limit) のはるかに外側にある。クワオアーの自転周期と3:1の軌道共鳴 (Quaoar 1/3 SOR) 、またはウェイウォットの公転周期と1:6の軌道共鳴 (Weywot 6/1 MMR) は、両者ともほぼ同じ距離となり (ring solutions 1 and 2) 、観測値とも一致する(Credit: Morgado, et.al.)】
クワオアーの環の存在を説明するには、これまでの環の形成理論とは異なる仕組みが必要となります。研究チームは、クワオアーからの距離がカギだと予想しています。発見された環の公転周期はクワオアーの自転周期の3倍、衛星ウェイウォットの公転周期の6分の1です。公転周期が他の天体の軌道要素と整数比になることは「軌道共鳴」と呼ばれ、整数比以外の値は不安定になることから、天体の公転軌道に制約をもたらします。クワオアーの環の場合、クワオアー本体の自転周期との3:1の軌道共鳴、または衛星ウェイウォットとの1:6の軌道共鳴が、環を1つの塊にまとめない原動力になっている可能性があります。実際に、クワオアーの環を構成する物質は均一に分布しているのではなく、細く高密度な部分の幅は5km、広く低密度な部分の幅は300kmと、密度と幅が一定ではないことが観測値から推定されています。軌道共鳴による環の物質のかき乱しは、環の不均一さをよく説明します。
クワオアーのロシュ限界の外側にある環が発見されたことで、環の形成理論は見直しを迫られています。例えば、ロシュ限界の内側にある他の天体の環の形成にも、軌道共鳴の影響が加わっている可能性があります。この可能性はハウメアで既に示唆されています。また、不均一な環は土星のF環などでも観測されていますが、この原動力も衛星との軌道共鳴だとする説があります。クワオアーの環の形成を考察することは、他の天体の環に関する謎の解明にもつながるかもしれません。
Source
・B. E. Morgado, et.al. “A dense ring of the trans-Neptunian object Quaoar outside its Roche limit”. (Nature)
・Tim Reid. “Getting to the Quaoar of planetary ring theory”. (Nature Middle East)
・George Dean. “A new ring system discovered in our Solar System”. (University of Sheffield)
文/彩恵りり
星食 (Lunar occultation)† 月はもっとも地球に近い天体であり、地球の周りを公転する間にさまざまな天体の前を通り過ぎます。 このように月が天体を隠してしまう現象を星食 (せいしょく) あるいは月による掩蔽 (えんぺい) と呼びます。
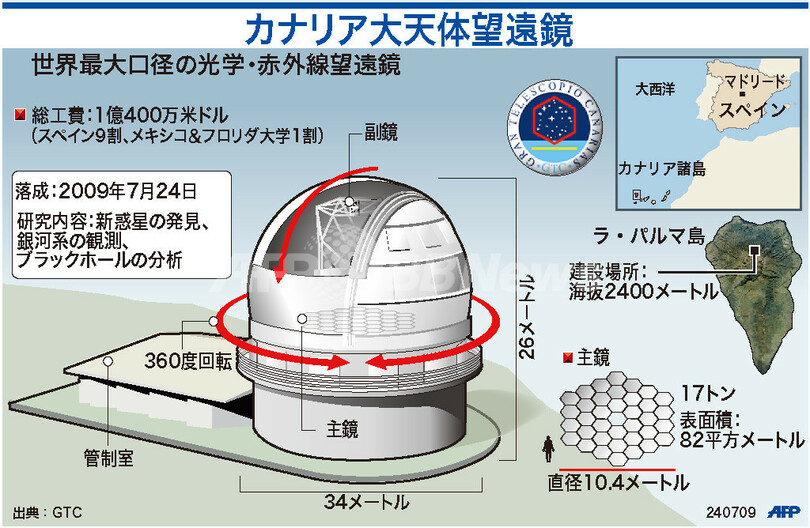
【図解】世界最大の口径、「カナリア大天体望遠鏡」
カナリア大望遠鏡(カナリアだいぼうえんきょう、Gran Telescopio Canarias、GTC)は、スペイン領カナリア諸島ラ・パルマ島のロケ・デ・ロス・ムチャーチョス天文台内にあり、しばしば GranTeCan と呼ばれる口径10.4mの反射式望遠鏡である。
| Gran Telescopio Canarias | |
|---|---|
 |
|
| 運用組織 | カナリア天体物理研究所, フロリダ大学, メキシコ国立自治大学 |
| 設置場所 | ラ・パルマ島 , スペイン |
| 座標 | 北緯28度45分24秒 西経17度53分31秒 |
| 標高 | 2,267 m (7,438 ft) |
| 建設 | 2002年 –2008年 年 |
| 観測開始年 | 2007年7月13日 |
| 形式 | 光学望遠鏡, リッチー・クレチアン式望遠鏡, segmented mirror, 望遠鏡 |
| 口径 | 10.4 m (34 ft 1 in) |
| 開口面積 | 78.54 m2 (845.4 sq ft) |
| 焦点距離 | 169.9 m (557 ft) |
| ウェブサイト | www |


望遠鏡は火山の山頂2267mに設置されている。7年がかりで建設された。GTC計画はスペイン、メキシコ、フロリダ大学、カナリア天体物理研究所 (IAC) の共同で設立された。建設費は13000万ユーロかかった。
軌道共鳴(きどうきょうめい、orbital resonance)とは、天体力学において、ある天体の周りを公転する2つの天体が互いに重力を及ぼし合う結果、両者の軌道が変化すること。 公転周期と同程度の短い時間スケールで影響する平均運動共鳴と、104 – 106 年の長い時間スケールで影響する永年共鳴がある。
中心天体の周りを公転する二つの天体が互いに重力を及ぼし合う結果、両者の軌道が変化すること。軌道共鳴により軌道は安定化する場合もあるが不安定になる場合もある。
公転周期の時間スケールで影響する平均運動共鳴と、それよりも遥かに長い時間スケールで影響する永年共鳴がある。


