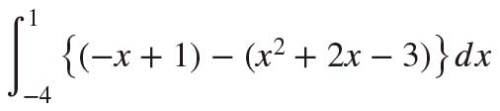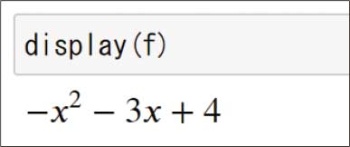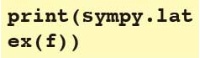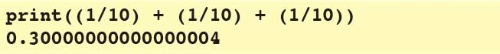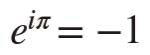超多機能電卓としても使えるPython、面倒な計算を手軽に実行
Pythonが普及することでプログラミングが身近になってきた。Pythonプログラミングを利用して数学を学んだり楽しんだりしていこう。
(3)超多機能電卓として使う
数学で計算は欠かせませんが、時に煩わしいものでもあります。そのようなときは、電卓を使ってもよいでしょう。Pythonの数式処理ライブラリである「SymPy」を使うと、因数分解や微分積分、方程式の解の計算などを簡単に行えます。言わば、Pythonが“超多機能電卓”になるのです。
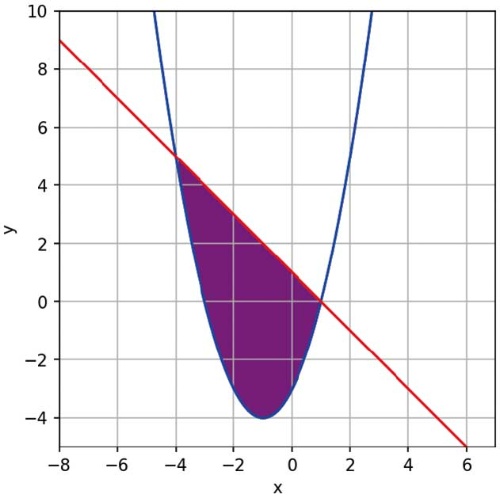
SymPyはAnaconda Distributionに含まれるので、すぐに利用できます。早速、図11の紫で塗りつぶされた領域の面積を求めてみましょう。
まず、「y = x2 + 2x - 3」と「y = -x + 1」の交点のx座標を求めます。これは、「-x + 1 = x2 + 2x - 3」の2次方程式を解けばわかりますから、SymPyを使ってリスト11のようなプログラムを作ります。実行すると、「[-4, 1]」と表示され、2つある交点のx座標が-4と1であることがわかりました。
これで図12の定積分で面積がわかるので、リスト12のようなプログラムを作ります。実行結果は「125/6」(6分の125)です。これが紫で塗りつぶされた領域の面積です。
リスト11とリスト12は最後の1行以外全く同じですから、まとめて解説しましょう。まず、冒頭でSymPyをインポートしたら、「symbols関数」を使って、数式で使う変数を定義しています。
これでxの数式を記述できるようになりました。
次に、このxを使って、「y = x2 + 2x - 3」と「y = -x + 1」の数式を作成しています。
続いて、「-x + 1 = x2 + 2x - 3」の2次方程式を次のように作成しています。
このfを「solve関数」に与えて、解を求めています。
その後、この解(-4と1)と「integrate関数」を使って定積分を行っています。
ちなみに、fに格納した数式は「display関数」を使うと、キレイに表示できます。
コードの実行結果は図13になります。
「latex関数」を使うと、図13のキレイな数式のLaTeXのコマンドを表示できます。
実行結果は「- x^{2} -3x + 4」になります。
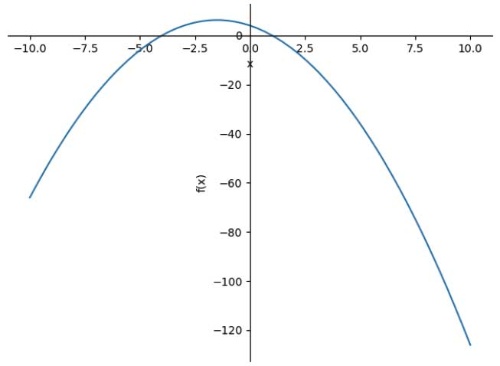
さらに、「plot関数」を使うと、fに格納した数式のグラフを描画できます。
実行結果は図14です。
バーゼル問題をSymPyで計算する
SymPyを使う大きなメリットの一つは、分数を分数のまま扱えることです。例えば、素のPythonで10分の1+10分の1+10分の1の計算を行うと、結果は分数にならないだけではなく、誤差も生じてしまいます(print関数のコードの下に実行結果を表示しています)。
一方、10分の1をSymPyの「Rationalクラス」を使って表現すると、計算結果は分数のまま表示されます。誤差もありません。
また、SymPyでは、文字を文字のまま扱う代数学的な計算を行えます。例えば、「オイラーの等式」(図15)を素のPythonで計算すると、次のようになります。
ちょっとわかりにくいのですが、計算結果は-1の近似値になっています。
では、SymPyだとどうなるでしょうか。
計算結果はキレイに-1になります。これはSymPyが、e(ネイピア数)やi(虚数)、π(円周率)を、sympy.E、sympy.I、sympy.piで代数学的に扱って計算できるからです。素のPythonの方の計算で使っているmath.eやmath.piは、無理数であるeやpiの近似値に過ぎません。近似値を使って数値計算しているので、結果も近似値になってしまうのです。
SymPyでは「sympy.oo」で無限大も扱えます。先ほど、コンピュータでは無限大を扱えないと書きましたが、SymPyだと代数学的に扱えます。
このsympy.ooを使うと、バーゼル問題を代数学的に計算できます。
計算結果はキレイに「pi**2/6」になりました。利用している「summation関数」はΣ(総和)の計算を行う関数です。
以上、3つの視点で、数学を学習する際のプログラミングの活用法を紹介しました。数学とプログラミングを行き来することで相乗効果が生まれ、両方のスキルを高めていくことができるのではないかと思います。