第8回　級数、整級数・関数の表現

前半では、基本的な数列の学習からはじめ、一般の数列の和を考え、さらに、無限個加えるときの状況を考察する。級数の収束・発散を理解し、判定することを目標とする。後半では、関数を項に持つ級数の収束・発散を学習する。更に、関数が級数で表現される範囲について学ぶ。級数や無限乗積で定義される特殊関数を紹介する。関数方程式への応用なども学習する。

【キーワード】
等差数列、等比数列、数列の和、級数、収束・発散、収束判定法、絶対収束、整級数、収束半径、関数項級数、無限乗積、関数方程式への応用

第8回展開2 講義Bの関連教材（PDF）

ダランベールの判定法

コーシー・アダマールの判定法

絶対収束

問題1の解答・解説

【問題】

正項級数

$\sum_{n = 1}^{\infty} \frac{n!}{n^{n + 1}}$

の収束・発散を調べよ。

選択肢　　　収束する

発散する

【解説】

正項級数ですから，収束するか，正の無限大に発散するかのいずれかです。解析学基本定理から，部分列が有界であることと収束することとが同値でであることがわかりますが，ここではダランベールの判定法を使って収束・発散を調べてみましょう。 $a_{n} = \frac{n!}{n^{n + 1}}$ として，適用します。

$\begin{aligned} lim_{n \to \infty} \frac{a_{n + 1}}{a_{n}} & = lim_{n \to \infty} \frac{\frac{(n + 1)!}{(n + 1)^{(n + 1) + 1}}}{\frac{n!}{n^{n + 1}}} = lim_{n \to \infty} \frac{\frac{(n + 1)!}{(n + 1)^{(n + 1) + 1}}}{\frac{n!}{n^{n + 1}}} = lim_{n \to \infty} \frac{\frac{n!}{(n + 1)^{(n + 1)}}}{\frac{n!}{n^{n + 1}}} \\ = lim_{n \to \infty} \frac{1}{{(\frac{n + 1}{n})}^{n + 1}} = lim_{n \to \infty} \frac{1}{{(1 + \frac{1}{n})}^{n} (\frac{n + 1}{n})} = \frac{1}{e} < 1 \end{aligned}$

となります。したがって，ダランベールの判定法から，あたえられた正項級数は収束することがわかります。

【解答】

収束する

この問題の関連教材
ビデオ：ダランベール判定法

PDF：ダランベール判定法

問題2の解答・解説

【問題】

正項級数

$\sum_{n = 1}^{\infty} \frac{2^{n}}{n^{n}}$

の収束・発散を調べよ。

選択肢　　　収束する

発散する

【解説】

前問同様に正項級数の判定ですから，収束するか，正の無限大に発散するかのいずれかです。ここでは，コーシー・アダマールの判定法を使って収束・発散を調べてみましょう。 $a_{n} = \frac{2^{n}}{n^{n}}$ として，適用します。

$lim_{n \to \infty} \sqrt[n]{a_{n}} = lim_{n \to \infty} \sqrt[n]{\frac{2^{n}}{n^{n}}} = lim_{n \to \infty} \frac{2}{n} = 0 < 1$

となります。したがって，コーシー・アダマールの判定法から，あたえられた正項級数は収束することが分かります。

【解答】

収束する

この問題の関連教材
ビデオ：コーシー・アダマールの判定法

PDF：コーシー・アダマールの判定法

問題3の解答・解説

【問題】

級数

$\sum_{n = 1}^{\infty} (- 1)^{n^{2} + 1} \frac{1}{n^{2}}$

は絶対収束するか調べよ。

選択肢　　　絶対収束する

絶対収束しない

【解説】

一見すると， $(- 1)^{n^{2} + 1}$ の部分が厄介そうですが，

$| (- 1)^{n^{2} + 1} \frac{1}{n^{2}} | = \frac{1}{n^{2}}$

ですので，級数

$\sum_{n = 1}^{\infty} \frac{1}{n^{2}}$

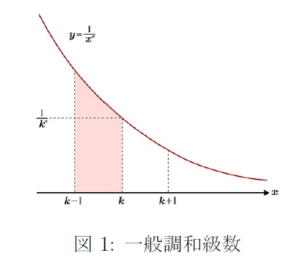
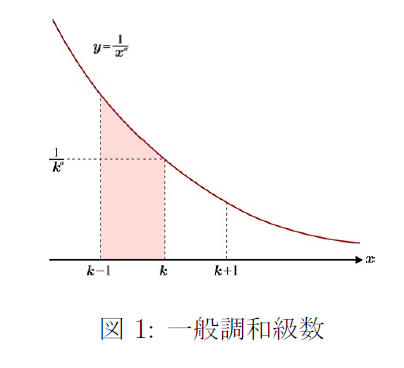
の収束・発散を調べればよいことになります。実際， $\sum_{n = 1}^{\infty} \frac{1}{n^{2}}$ は収束します。第8回の展開1の標準問題の中でも解説をしましたが，級数 $\sum_{n = 1}^{\infty} \frac{1}{n^{2}}$ の収束については，以下のように説明することができます。

$\begin{aligned} \frac{1}{2^{2}} + \frac{1}{3^{2}} < \frac{1}{2^{2}} + \frac{1}{2^{2}} = \frac{2}{2^{2}} = \frac{1}{2} \\ \frac{1}{4^{2}} + \frac{1}{5^{2}} + \frac{1}{6^{2}} + \frac{1}{7^{2}} < \frac{1}{4^{2}} + \frac{1}{4^{2}} + \frac{1}{4^{2}} + \frac{1}{4^{2}} = \frac{4}{4^{2}} = \frac{1}{4} = \frac{1}{2^{2}} \\ \frac{1}{8^{2}} + \frac{1}{9^{2}} + \dots + \frac{1}{15^{2}} < \underset{8 個}{\underset{⏟}{\frac{1}{8^{2}} + \frac{1}{8^{2}} + \dots + \frac{1}{8^{2}}}} = \frac{8}{8^{2}} = \frac{1}{8} = \frac{1}{2^{3}} \\ \dots \dots \dots \\ \frac{1}{(2^{n})^{2}} + \dots + \frac{1}{(2^{n + 1} - 1)^{2}} < \underset{2^{n} 個}{\underset{⏟}{\frac{1}{(2^{n})^{2}} + \dots + \frac{1}{(2^{n})^{2}}}} = \frac{1}{2^{n}} \end{aligned}$

したがって，各項は正ですから，級数 $\sum_{n = 1}^{\infty} \frac{1}{n^{2}}$ の部分和 $S_{n}$ について

$S_{n} < \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + \dots + \frac{1}{2^{k}} + \dots < \frac{1}{1 - \frac{1}{2}} < 2$

と評価されます。ゆえに ${S_{n}}$ は上に有界な増加列であることがわかります。したがって，解析学の基本定理から $S_{n}$ は収束します。以上より，問題にあたえられた級数は絶対収束します。

【解答】

絶対収束する

この問題の関連教材
ビデオ：絶対収束

PDF：絶対収束

Pocket