第2回 関数、 単調関数・逆関数
第2回 関数、 単調関数・逆関数
単調関数 たんちょうかんすう
x1<x2 ならば f(x1)≦f(x2)
であるとき、f(x)はこの区間で単調増加であるという。もし、ここで、つねにf(x1)<f(x2)であるときは、単に増加(または狭義の増加)関数という。たとえば、
f(x)=x (-∞<x<+∞)
f(x)=x2 (x≧0)
などは増加関数である。また、
f(x)=[x] (-∞<x<+∞)
も単調増加関数である()。
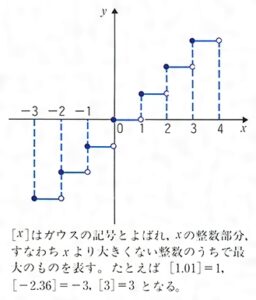
ここで[x]はxの整数部分、すなわちxより大きくない整数のうちで最大のものを表す。[x]はガウスの記号とよばれている。このように全区間がいくつかの区間に分けられ、各小区間の上では定数値をとりながら増加していくような関数を階段関数という。
単調増加関数は次のような性質をもつ。
(1)単調増加関数は、かならずしも連続ではないが、不連続である点は、たかだか可算個で、不連続点においては、左側からの極限値、右側からの極限値を有する()。
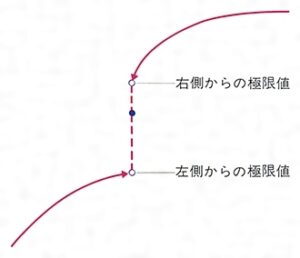
(2)連続な増加関数は逆関数を有し、逆関数もまた連続、増加である。
(3)単調増加関数は、ほとんどすべての点で、すなわちルベーグ測度が0であるような集合上を除いて微分可能である。
(4)f(x)がすべての点の上で微分可能で、f′(x)≧0ならばf(x)は単調増加である。
(5)単調増加関数は、リーマン積分可能である。
(6)区間[a,b]上の単調増加関数f(x)は、[a,b]上でフーリエ級数に展開できる。すなわち、そのフーリエ級数は、すべての点で収束し、f(x)の連続点では、その値はf(x)に等しい。これはフーリエ級数論において、ディリクレが印(しる)した第一歩であった(1829)。
単調増加関数の差として表される関数を有界変動関数という。これは次のような性質で特徴づけられる。c,d(c<d)を定義域のなかの任意の2点とすれば、ある正数Mがあって、
c=x0<x1<x2<……<xn=d
というような点x1,x2,……,xn-1をどのようにとっても
|f(x1)-f(x0)|
+|f(x2)-f(x1)|
+……+|f(xn)-f(xn-1)|≦M
となる。
[竹之内脩]

単調増加関数〔図A〕
単調増加関数の性質〔図B〕
2-10 問題★(基本)
単調関数,無理関数,逆関数についての練習問題です。
増加関数と減少関数とを総称して単調関数という。 とくに,x1<x2なるかぎりf(x1)<f(x2),またはf(x1)>f(x2)となるとき,それぞれf(x)は狭義単調増加,または狭義単調減少であるといい,これらの場合を総称して狭義単調であるという。 関数の単調性は,その定義域の一部の区間についていうこともある。…
f(x)=√x-2の微分の答えと解き方を教えてください!
数3逆関数の問題です。
関数f(x)=(3x+2)/(x+2)について、f-1(x)=xを満たすxの値を求めよ。
自然対数 ln、自然対数の底 e とは?定義や微分積分公式