データ分析に欠かせない「データのばらつき」を理解する
近年データ分析に取り組む企業が増えた結果、データサイエンティストという職業が注目されています。ところが実際の業務内容や必要な知識については、意外に知らない人も多いものです。そこで本特集では書籍『ビジュアル データサイエンティスト 基本スキル84』(日経BP 日本経済新聞出版)から厳選し、知っておきたいデータサイエンティストの基礎知識をお届けします。
今回は、書籍『ビジュアル データサイエンティスト 基本スキル84』で紹介した基礎知識の中から「分散」と「中心極限定理」を見ていきましょう。
前回までの記事:今どきの「読み・書き・そろばん」となった統計学の基礎を押さえよう
分散
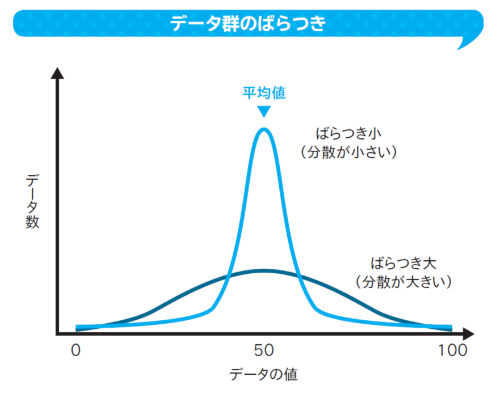
データがどのくらい散らばっているのかを1つの指標で表したものが「分散」です。
分散は、各データが平均値からどれぐらい離れているのかを計算することで求めます。まずは、各データと平均値の差を求めます。単純な差だけでみると、プラスの場合とマイナスの場合があり、すべてプラスの値とするために、この差を2乗します。これをデータの数だけ計算して、その和を求め、データの個数で割ります。
言い換えると、分散は、「各データと平均値の差分を2乗したものの平均」と言えます。各データが、平均的に、どれぐらい平均値から離れているのかを指標化したものです。
平均値から大きく離れたデータの場合は、各データと平均値の差が大きくなります。このようなデータが多い場合には、分散が大きくなり、データのばらつきは大きいといえます。ばらつきの度合いを1つの指標でわかりやすく表現できます。
分散は計算の過程でデータを2乗しているため、単位の意味がわかりにくいのが欠点です。そのため、分散の平方根(ルート)をとることで、2乗した単位をもとに戻したものが「標準偏差」です。わかりやすく表記するために、標準偏差を表す記号としてはσ(シグマ)、分散を表す記号としてはσ2が使われます。
入試などで使われる偏差値は「10 ×(自分の点数-平均点)÷ 標準偏差 + 50」で計算されます。
中心極限定理
母集団の特徴を把握するために、標本を抽出して、平均や分散を計算しますが、標本数が少なければ正しく推計することはできません。日本人全体の平均身長を求める際に、例えば100人の標本だけで計算した結果では誤差が大きいことは想像できるでしょう。では、1万人の標本であればどうでしょう。100人と比べれば、1万人の場合は、より正確に計算できていることになるでしょう。
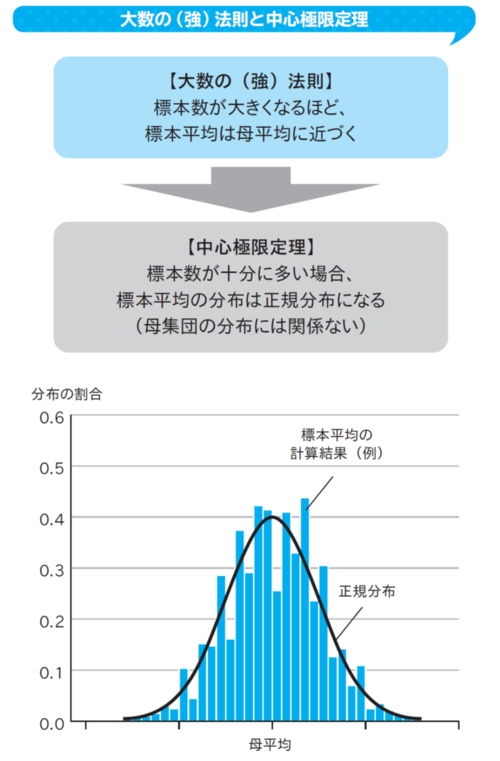
母集団から抽出する標本数が多いほど、母集団の特徴を正確に推定できるようになります。ある母集団の中から無作為に抽出した標本の平均は、標本数を多くすれば、母集団の平均(母平均)に近づきます。これを「大数の法則」(厳密には「大数の強法則」)と言います。
「中心極限定理」とは、標本数が十分に多い時に標本平均は正規分布に従うという定理です。無作為に1万人選び平均身長を計算する、また別の1万人を選ぶ……ということを繰り返し行った場合、その計算結果の分布は正規分布になるのです。また、その正規分布の平均値は母平均と同じ値になります。母集団がどのような分布であっても中心極限定理は成り立つため、この特集で後ほど紹介する検定などの基礎になります。
正規分布とは、下図のようなグラフの形で、データが平均値周辺に集まる形をしています。正規分布の中でも、平均が0、分散が1であるものを標準正規分布と呼びます。